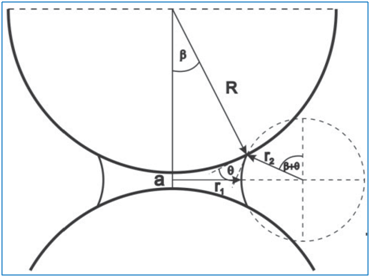
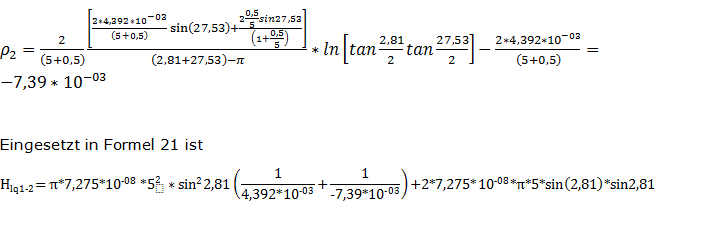Für diesen Kontaktfall tritt die maximale Haftkraft einer Flüssigkeitsbrücke zwischen zwei kugelförmigen Partikeln mit unterschiedlichen Durchmessern DP1 und DP2 und Radien R1 und R2 auf, wenn die beiden Benetzungswinkel und der Randwinkel gegen Null gehen. Sie beträgt:

Damit ist die maximale Haftkraft Hlq1-2,max zwischen einem großen und einem kleinen Partikel immer geringer als die maximale Haftkraft Hlq1 1,max zwischen zwei großen Partikeln. Für den Fall R2 = R1 wird Formel 17 zu Formel 16.

Nach [92] ist der Brückenwinkel

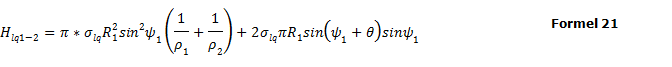
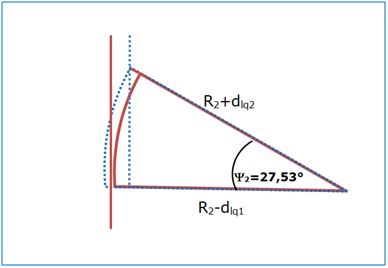
O.a. Formeln [92] beschreiben den Kontaktfall der Partikel, ein Abstand a ist darin nicht berücksichtigt. Der für die Berechnung der Haftkraft Hlq1 2 erforderliche Brückenwinkel Ψ2kann für zwei unterschiedlich große Partikel mit zwei unterschiedlich dicken Wasserfilmen berechnet werden zu:

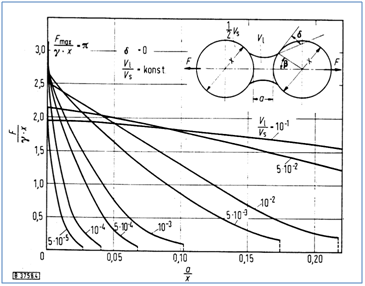
In Kap. 2.4.2.1 wurden die Kräfte durch Adsoptionsschichten auf den Partikeloberflächen beschrieben. Wenn genügend Wasser zur Verfügung steht, um eine Filmdicke auszubilden, die größer ist als die Distanz des adsorptiv mit hohen Haftspannungen an der Oberfläche gebundenen Wassers, dann können sich Flüssigkeitsbrücken (sog. Zwickelkapillare) zwischen benachbarten Partikeln bilden. Bei konstanter Oberflächenspannung der Flüssigkeit ist die Höhe der Haftkraft von der geometrischen Situation der Flüssigkeitsbrücke und dem Brückenvolumen abhängig.Ein wesentlicher Faktor, der die Zugfestigkeit von Feuchtagglomeraten beeinflusst, ist das Verhältnis von Partikelabstand a zu Durchmesser d bzw. x wie in Abbildung 59dargestellt. Auch das absolute Verhältnis des Volumens Flüssigkeit Vl zum Volumen Feststoff VS (Vl/VS) beeinflusst die Kapillarkraft:
Abbildung 59: Kapillarkräfte in einer Flüssigkeitsbrücke:Einfluss von Abstandsverhältnis und Brückenvolumen auf die Haftkraft [88] (Fmax = σlq*×*d)
Mit kleiner werdendem Abstandsverhältnis a/x nimmt die Haftkraft zwischen den Partikeln zu. Anders ausgedrückt reagiert die Haftkraft mit kleiner werdendem relativen Brückenvolumen empfindlich auf Abstandsänderungen, der Abriss der Brücke erfolgt bei umso geringeren Dehnungen, je geringer das Brückenvolumen Vlist. Wird eine Brücke gedehnt, so wird sie bei Erreichen des kritischen Abstandes instabil und platzt. Je kleiner die Brücke ist, umso früher tritt Instabilität auf. Der kritische Abstand kann bereits auch durch Mikrorauhigkeiten (Spitzen und Täler) an den Kontaktstellen erreicht werden, wodurch die Haftkraft genauso verringert wird wie durch Dehungen der Brücke selber [125]. Da in der Praxis keine absolut glatten Teilchenoberflächen vorliegen, kommt der Fall a = 0 mit großer Wahrscheinlichkeit nicht vor. Es stellt sich ein scheinbarer Abstand a´ ein, der durch die Rauhigkeitserhebungen bestimmt ist. a´ sollte nach [125]für Teilchen verschiedener Größe des gleichen Stoffes annähernd gleich sein.Daraus ergibt sich, dass der Einfluss der Rauhigkeiten mit zunehmender Partikelgröße abnimmt, da der Quotient a/x geringer wird. Bei kleinen Partikeln wird die Haftkraft durch die Oberflächenrauhigkeiten deutlicher verringert als bei größeren Partikeln.
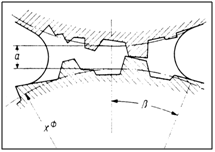
Abbildung 60: Flüssigkeitsbrücke zwischen realen Teilchen mit scheinbarem Abstand a´ [125]
In Abhängigkeit der mittleren Rauhigkeit und der Dicke der adsorbierten Wasserschicht nimmt die Haftkraft der Flüssigkeitsbrücke ab, da sich der Abstand der Partikel vergrößert und gleichzeitig die zu benetzende Oberfläche der Partikel zunimmt. Bei einer konstanten Wassermenge bildet sich daher ein dünnerer Wasserfilm um die Partikel aus und das Brückenvolumen nimmt ab [85]. Da dann das Abstandsverhältnis a/x mit größer werdender Teilchengröße abnimmt, werden die Zugfestigkeitswerte bei Flüssigkeitsfüllungsgraden, die isolierte Brückenmodelle zulassen, zunehmen.
Bei der Berechnung der Haftkräfte durch Flüssigkeitsbrücken wird in der Regel von gleichgroßen Kugeln ausgegangen, zwischen denen eine einzelne, isolierte und symmetrische Flüssigkeitsbrücke existiert, wie sie in Abbildung 61 dargestellt ist [88].
Abbildung 61: Flüssigkeitsbrücke zwischen zwei gleich großen, ideal glatten Kugeln [88]
Die Bindung ist auf die Kapillarkraft durch den kapillaren Unterdruck in der Flüssigkeitsbrücke und auf die Randkraft längs des Dreiphasenkontaktes Partikel Wasser Luft (Oberflächenspannung) zurückzuführen. Es sind gerade soviele Flüssigkeitsanteile vorhanden, dass sich ein Verhältnis wie in Abbildung 47b) einstellt. Wenn die Zwischenräume völlig mit Flüssigkeit ausgefüllt sind wie in Abbildung 48b), so wirkt nur ein kapillarer Unterdruck, da keine Dreiphasenkontakte existieren.
Für den Fall idealer, isolierter Flüssigkeitsbrücken wie er in der Abbildung 61 und Abbildung 62 dargestellt ist, ergibt sich die Haftkraft der Flüssigkeitsbrücke Hlq aus den Anteilen der Randkraft σRinfolge Oberflächenspannung und der Kapillarkraft zu
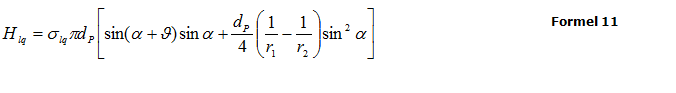


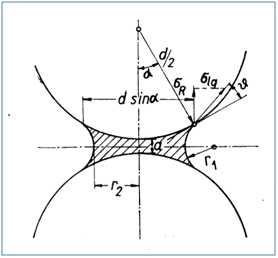
Der jeweils bezogen auf die Flüssigkeit konvexe Azimutradius r2 und der konkave Meridionalradius r1 können nach [90] aus der geometrischen Situation vonAbbildung 62abgeleitet werden:
Abbildung 62: Zweidimensionale Darstellung der Flüssigkeitsbrückengeometrie für den Kontaktfall gleich großer Kugeln mit Abstand ain Anlehnung an [90] mit Randwinkel ℘, d.h. ohne Adsorptionsschichten an den Oberfläche
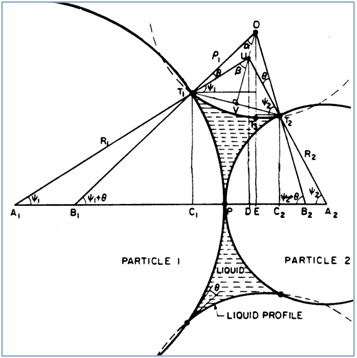
Abbildung 63: Flüssigkeitsbrücke zwischen Partikeln unterschiedlicher Größe [92] ; mit Ψ1,Ψ2.als unterschiedliche Benetzungswinkel, θ als Randwinkel
Die Hauptkrümmungsradien der Flüssigkeitsbrücke berechnen sich zu [90]:



Je kleiner das Brückenvolumen, desto größer ist die Haftkraft, deren Maximum lediglich von dem Partikeldurchmesser abhängig ist.Wenn beide Partikel deutlich größer sind und einen Durchmesser von 10 µm aufweisen bei unverändertem Abstand und Schichtdicken,dann wird die Haftkraft ansteigen, da das Verhältnis Vl/VS (Brückenvolumen zu Feststoffvolumen) insgesamt 2000 mal kleiner ist als bei zwei Partikeln von 1µm und das Verhältnis a/x bzw. a/DP ebenfalls 10 mal kleiner ist.
Für andere geometrische Verhältnisse als in Abbildung 61 bzw. 57 ist eine Berechnung der Haftkraft nur schwer möglich. Die mit Formel 12angegebenen Zusammenhänge gelten für gleich große Kugeln mit ideal glatter Oberfläche. Die überwiegende Zahl der Arbeiten auf dem Gebiet geht von diesen vereinfachenden Annahmen bei der Ableitung der theoretischen Haftkräfte aus [92].
Bei unterschiedlich großen Partikeln, wie sie in den meisten Partikelverteilungen wie z.B. Zement, Flugasche oder Kalksteinmehl vorkommen, ist die Berechnung des Brückenvolumens relativ aufwendig [91]. Für unterschiedlich große Partikel finden sich komplexere Ansätze für die Berechnung. Auf Mehrotra und Sastry [92] geht ein Ansatz zurück, der den Fall von Flüssigkeitsbrücken zwischen Partikeln unterschiedlicher Größe berücksichtigt, wie er bei statistischen Partikelverteilungen vorkommt.
Abbildung 64: Detail der geometrischen Kontaktsituation zweier Partikel mit Wasserfilmen von jeweils 0,03 µm
Als Beispiel dientder Partikelkontakt, der in Kap. 2.4.2.1 bei der Berechnung der Adsorptionskraft angenommen wurde, die Partikel 1 und 2 sind in Abbildung 64 als stark vergrößerter Ausschnitt dargestellt: