In den Kontaktpunkten von Partikeln in einem Schüttgut oder einem Erdstoff können die bereits erwähnten Kräfte sowie äußere Kräfte als Normalkräfte übertragen werden. Wer den die Partikel gegeneinander verschoben, treten zusätzlich Schubspannungen auf, die einer Verschiebung entgegen wirken.
Der Widerstand gegen die Verschiebung setzt sich aus folgenden drei Komponenten zu sammen [112]:
1. Reibungswiderstand auf der Oberfläche der Körner
2. Umordnung durch gegenseitige Verdrehung und Verzahnung der Körner
3. durch Anheben verbundene Volumenvergrößerung (Dilatation)
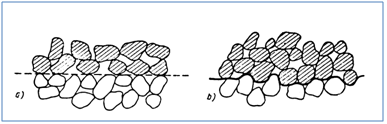
Bei dieser Art der Kraftübertragung handelt es sich um Kräfte, die ohne äußere Einflüsse zwischen Partikeln nicht wirken. Vielmehr wirken Reibung und Verzahnung erst dann kraftübertragend, wenn Verschiebungen zwischen den Partikeln stattfinden und sich durch Reibung und Verzahnung ein Widerstand gegen die Verschiebungsrichtung ausbil det. Abbildung 74verdeutlicht die Komponenten am Beispiel eines unterschiedlich dicht gelagerten Sandes.
Abbildung 74: Scherwiderstand in einem körnigen Erdstoff [30],
a) Reibung auf der Oberfläche der Körner;b) Verzahnung der Körner
Der Reibungswiderstand wirkt der Gleitung eines Korns auf dem anderen entgegen und ist von der Oberflächenrauhigkeit der Körner abhängig. Die Verzahnung der Körner nimmt mit der Dichte der Lagerung zu, da die Körner zueinander eine engere Position einnehmen und ein Anheben der Körner erforderlich ist, um eine seitliche Bewegung durchzuführen. Dadurch kommt es zu einer Volumenvergrößerung (Dilatation) des dicht gelagerten Schüttgutes. Die Dilatation ist umso größer, je ungleichförmiger die Einzel körner in der betrachteten Gesamtmatrix sind. Die Ungleichförmigkeit ist ein Kennwert für den Größenunterschied der Körner einer Matrix. Der Widerstand gegen Verdrehen bei gegenseitiger Verzahnung ist bei kantigen und unregelmäßig geformten Körnern größer als bei ideal runden Körnern [51], [30], [121]. Die Schubspannungen, die aufgrund des Gesamtwiderstandes von der Matrix der Körner aufgenommen werden können und den Verschiebungen entgegenwirken, sind von der Höhe der Normalkraft abhängig, die in den Kontakten der gegeneinander verschobenen Körner wirkt.Die graphische Darstellung in dem aus der Bodenmechanik geläufigen σ- ī-Diagramm (siehe Abbildung 34) zeigt unter der Annahme des Bruchkriteriums nach Coulomb eine steigende Gerade, deren Winkel der innere Rei bungswinkel der Kornmatrix ist und von den drei o.g. Mechanismen abhängt.Bei größe ren Normalspannungen(σ > 0,5 N/mm2) ist der lineare Zusammenhang nicht mehr gültig und der Reibungswinkel nimmt ab.
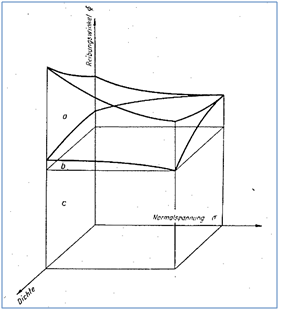
Die Abhängigkeit von der Normalspannung und der Dichte der Kornmatrix ist inAbbildung 75beispielhaft für einen Sand dargestellt [112].
Abbildung 75: Veränderung der Anteile des Reibungswinkels mit der Normalspannung
und derDichte [122](Dilatation (a), Umordnung (b), Korn-zu-Korn-Reibung (c))
Der Anteil c), die Korn-zu Korn-Reibung, ist konstant und unabhängig von der Dichte und der Normalspannung. Der Anteil der Umordnung der Körner am Reibungswinkel ist bei geringer Dichte am Größten, dann steht innerhalb des Feststoffes mehr Raum zur Verfü gung. Der Anteil der Dilatation dann am geringsten, weil bei geringen Dichten ausreihend Raum innerhalb der Matrix für eine Umordnung ohne Volumenvergrößerung (Dilatation) zur Verfügung steht. Sie kommt zum Tragen, wenn hohe Dichten und geringe äußere Spannungen vorherrschen. Bei hohen Dichten liegt der Anteil der Dilatation immer ein Vielfaches über dem Anteil aus Umordnung. Beide zusammen sind in etwa so groß wie der Anteil aus der Korn-zu-Korn-Reibung.
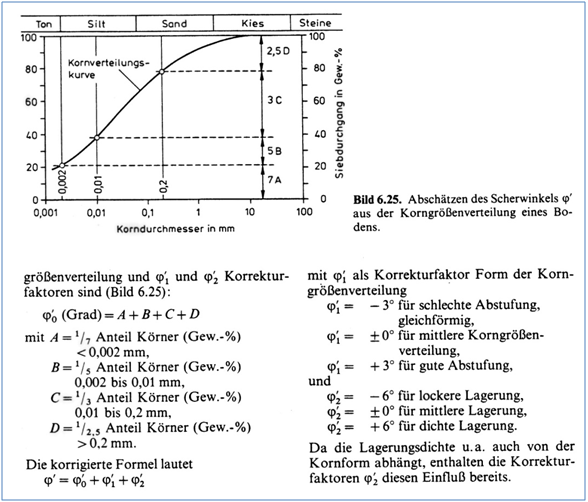
Eine Abschätzung des Reibungswinkels ist inAbbildung 76 wiedergegeben.
Abbildung 76: Abschätzen des Scherwinkels eines Bodens aus der Korngrößenverteilung [112]
Über mehrere Größenordnungen der Korngrenzen hinweg gilt, dass der Reibungswinkel abnimmt, je feiner die Bestandteile der Matrix zusammengesetzt sind. So ist der Rei bungswinkel von Sand geringer als von Kies. Bei grobem Kalksteinmehl (Korngröße 20 45µm) hat Molerus [102] durch Zugabe von feinem Kalksteinmehl (Korngröße 3,4 7µm) nachgewiesen, dass der innere Reibungswinkel mit steigendem Feinanteil ebenfalls ab nimmt und bei ca. 30 M.-% Feinanteil das Grobgut keinen Einfluss ausübt. Der Rei bungswinkel entsprach dem der reinen Feinkornschüttung.
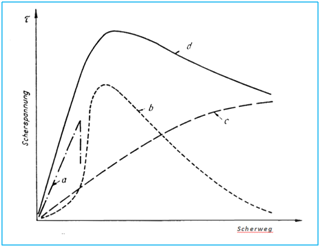
Auch bei der Bestimmung des Scherwiderstandes werden die in Kap. 2.4.2.2 2.4.2.6 beschriebenen Mechanismen, die Haftkräfte auslösen, bereits bei sehr kleinen Scherver schiebungen aktiviert. Aufgrund der recht geringen Reichweiten der einzelnen Haftkraft komponenten endet die Haftfestigkeit bei Überschreiten der einzelnen Reichweiten, bevor die Reibungseffekte ihren Höhepunkt erreichen. Dies ist in Abbildung 77 erkennbar.
Abbildung 77: Änderung der Komponenten des Scherwiderstandes mit zunehmender
Scherverschiebung : a) Haftfestigkeit, b) Dilatation, c) Reibungseffekte,d) Summenkurve gemessener Werte [112]
Da sich die Darstellung auf feuchte Sande bezieht, bei denen der Scherwiderstand unter Auflast in eine Scherzelle gemessen wurde, ist das Resultat nur bedingt auf zentrische Zugfestigkeit und auf deutlich kleinere Partikelsysteme übertragbar. Dies ist insbeson dere daran zu erkennen, dass die Reibungseffekte mit dem Weg immer weiter zuneh men. Auch handelt es sich bei dem abfallenden Ast der Kurve d) nicht um eine Resttrag fähigkeit, sondern um den verbleibenden Anteil an Widerstandskomponenten, der er kennbar gegen c) konvergiert. Bedeutsam ist jedoch, dass die Haftfestigkeit sehr rasch und stark zunimmt und auch wieder abfällt, die Dilatation verzögert und dann schlagartig einsetzt um dann langsam abzufallen.
Bornemann [22] stellte im Rahmen seiner Untersuchungen an erdfeuchten Betonen bei Druckversuchen an vollständig ausgetrockneten Feinkorngemischen die höchsten Druck festigkeiten fest und zog als Ursache die höheren Reibungs- und Verzahnungswider stände im Vergleich zu feuchteren Gemischen heran.Zeh [123] führte umfangreiche Zug versuche an bindigen Böden durch. Bei seinen Versuchen und auch bei den diskutierten Literaturergebnissen zeigte sich, dass die Zugfestigkeit bei abnehmenden Wassergehalten stark ansteigt. Nach [123] sind jedoch Effekte wie die Meniskenumkehr (Oberflächenspannungshysterese) dafür verantwortlich, da die zentrischen Zugversuche nicht derartig stark von Reibungseffekten der Partikel untereinander abhängen können.
Zementpartikel, ebenso wie Flugasche, Silika und Kalksteinmehle weisen an ihren Ober flächen Rauhigkeiten auf. Dadurch entsteht eine Reibung dieser Rauhigkeiten aneinan der, wenn sich die Oberflächen voneinander entfernen durch eine äußere aufgebrachte Zugkraft. Wenn Partikel unterschiedlicher Materialien also z.B. glatte Oberflächen haben und andere rauhe, dann werden die rauhen Oberflächen bei bereits eingesetzten Verfor mungen der Matrix durch aufgebrachte Zugkräfte dann einen höheren Widerstand gegen die Verformung, d.h. die Vergrößerung der Partikelabstände, entgegensetzen können als glattere. Auch werden die Haftkräfte zwischen glatten Oberflächen größer sein, da der wirksame Kontaktabstand geringer ist. Weil die Wege bei Zugversuchen deutlich geringer sind als bei Druck- und Scherversuchen, werden die Reibungskräfte nur einen sehr geringen Beitrag über eine sehr kurze Distanz hinweg stellen können.
Eine Verzahnung und Verdrehung der Körner unter Beibehaltung ihrer Lage, also ohne Dilatation, findet statt, wenn die Bruchebene z.B. um den halben Umfang eines Partikels oder noch weiter, herumführt.Hierfür wird in der Matrix Platz benötigt, daher ist dieser Anteil bei geringeren Dichten größer als bei den vorherrschenden, hohen Packungsdich ten erdfeuchter Leimgemische. Dilatation tritt am stärksten bei hohen Dichten auf, dabei vergrößert sich die Bruchfläche. Bommes [134] hat in umfangreichen Messungen der tatsächlichen Bruchfläche an zentrischen Zugversuchen erdfeuchter Zementleime nach-gewiesen, dass es zu relativ konstanten Abweichungen von der idealen geringsten Bruchfläche kommt, die Vorgehensweise wird in Kap. 4.1.4 beschrieben.
Abbildung 78: Ermittlung der tatsächlichen Bruchflächen beim zentrischen Zug an erdfeuchten Zementleimen durch Frischhaltefolie und anschließender manueller
Flächenauszählung nach Bommes [134]
Die allgemein auftretende, recht konstante Erhöhung des Bruchquerschnittes deutet auf Effekte der Dilatation hin. Auch ist in Abbildung 78 erkennbar, dass der Bruch im Zementleim nicht ideal eben erfolgt ist.Insbesondere bei Zementleimen mit höheren Wassergehalten war erkennbar, dass sie ein duktileres Verhalten zeigten als trockenere, siehe Abbildung 79.
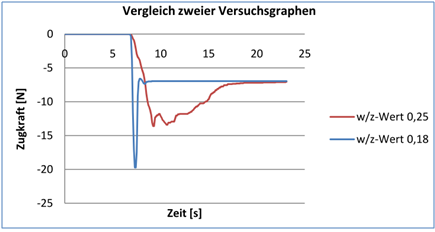
Abbildung 79: Vergleich von zwei Zementleimen [134]
Bommes beschreibt eine höhere Zementleim Dehnbarkeit, die er auch bei den Reini gungsvorgängen der Schalung beobachten konnte, indem Leime mit höheren w/z Werten sich augenscheinlich verformbarer verhielten. Auch nach dem Überschreiten der Maximalkraft führten diese Leime noch zu einem duktilen Verhalten, sie nehmen weiterhin Kräfte auf bei Zu nahme der Wege.
Abbildung 80: Bruchbild nach zentrischem Zugversuch zweier erdfeuchter Zementleime, links w/z=0,18, rechts w/z=0,25. [132]
Der Unterschied der Bruchbilder ist in Abbildung 80 erkennbar. Während der rechte Bruch querschnitt auch geböschte bzw. annähernd senkrechte Bereiche beinhaltet, ist der linke Querschnitt vergleichsweise eben verlaufen. Dies deckt sich mit dem unterschied lichen Verhalten der Kurven in Abbildung 79.Ob es sich um Effekte aus Dilatation han delt oder um beobachtete Dehnungen von Flüssigkeitsbrücken wie sie in Kap.2.4.2.3 beschrieben wurden handelt, oder einer Kombination, kann nicht sicher bestätigt wer den.
Bei der Bestimmung der zentrischen Zugfestigkeit einer Partikelmatrix handelt es sich um einen isostatischen, einachsigen Zugversuch, bei dem idealerweise nahezu keine Schub kräfte auftreten. Dadurch kann auch kein Reibungswinkel aktiviert werden, und die Er kenntnisse aus Schubversuchen Abbildung 77sind nicht exakt übertragbar. Zudem sind die Wege bei der Prüfung von Zugfestigkeiten sehr gering, so dass für die Aktivie rung der mechanischen Widerstände nur sehr geringe Verformungen zur Verfügung ste hen, bevor es zum Bruch und damit zum Kontaktverlust kommt. Dennoch werden die beschriebenen Anteile, die in ihrer Summe den schubspezifischen Reibungswinkel bilden, auch in etwas geringerer Form bei zentrischen Zugversuchen in der Lage sein, der Ver formung einen Widerstand entgegen zu setzen.
Anders als bei den vorgestellten Mechanismen der Haftkräfte ist es nicht möglich, anhand von Beispielen einen konkreten Anteil der Reibung, Verzahnung und Dilatation an der Zugfestigkeit zu berechnen. Jedoch können die erläuterten Mechanismen des Reibungs winkels dazu beitragen, den relativen Einfluss abzuschätzen.
Auf eine detailierte Beschreibung der Versuche zur Ermittlung des Reibungswinkels an dieser Stelle wird hier verzichtet und auf die Literatur verwiesen [124].