Damit aus den theoretischen Überlegungen zu den wirkenden Haftkräften zwischen ein zelnen Partikeln die Zugfestigkeit einer Partikelpackung berechnet werden kann, müssen Annahmen über die Kräfte und über die Kontaktflächen im Bruchquerschnitt getroffen werden. Zur Theorie der Zugspannungen in Agglomeraten existieren unterschiedliche Ansätze. Allen gemeinsam ist die Grundlage, über das Integral der Haftkräfte pro Partikel auf die Gesamthaftkraft in dem betrachteten Agglomeratquerschnitt zu schließen und damit die Zugspannung auszudrücken, die in einem Agglomerat wirkt.
Die Unterschiede in den Theorien liegen in den berücksichtigten Kraftarten, die zwischen den Partikeln übertragen werden und der Art und Weise, wie das Integral der Haftkräfte über die Fläche angenähert wird.Dabei spielt die Koordinationszahl, welche die Berüh rungspunkte der Partikel untereinander angibt, eine große Rolle. Sie wird dadurch beein flusst, ob monodisperse Partikel vorausgesetzt werden, oder ob Partikelverteilungen n(x) berücksichtigt werden.Entsteht in einem Partikelagglomerat ein Bruch infolge äußerer Zugkraft, verläuft die Bruchfläche entlang der Partikelgrenzen. Ein Bruch innerhalb der Partikel scheidet aufgrund der geringen Zugkräfte aus.
Wierig [20] berechnete in seinem Modell die Druckfestigkeit erdfeuchter Betone anhand der Zugspannung in der Betonmatrix. Dabei berücksichtigte er ausschließlich Haftkräfte durch Flüssigkeitsbrücken zwischen den Zementpartikeln. Die Zugfestigkeit berechnete er dabei aus der lockersten Lagerung der Zementkörner (kubische Verteilung mit dem Parti keldurchmesser d als Seitenlänge, dabei bilden vier Partikel einen Würfel mit der Kantenlänge 2*d) unter der Annahme einer monodispersen Partikelverteilung mit dem mittleren massenbezogenen Korndurchmesser des Zementes mit
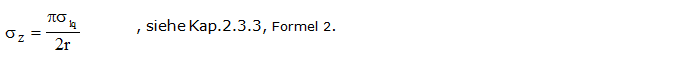
Dabei wird die maximale Haftkraft einer Flüssigkeitsbrücke angesetzt, die dann auftritt, wenn die Ausdehnung der Brücke punktförmig ist und der Winkel des Oberflächenseg-mentes der Brücke auf der Kugeloberfläche gegen Null geht.
Auf Rumpf [125], [126] geht ein weit verbreiteter Ansatz zurück, der die realen Verhält nisse in einer Partikelmatrix besser berücksichtigt.
Ausgehend von der Vorstellung, dass die Festigkeit eines Agglomerates an den Kontakt stellen zwischen den agglomeratbildenden Teilchen durch die dort herrschenden Binde kräfte übermittelt wird, ergibt sich, dass die Zugfestigkeit von der Zahl der Teilchen im Querschnitt, der Anzahl der Berührungsstellen je Korn (Koordinationszahl k) und von der Haftkraft je Berührungsstelle abhängt.

• gleichmäßige Zufallspackung der Partikel, d.h. Volumenporosität =Flächenporosität
• Bindkräfte an den Kontaktpunkten schwanken um einen Mittelwert, durch den sie er
setzt werden können
• gleichmäßige, zufällige Verteilung der Kontaktpunkte
• agglomeratbildende Teilchen sind gleich große Kugeln
Im Gegensatz zu Wierig nähert Rumpf durch k und ∈ die tatsächlichen Lagerungsbedin gungen der Partikel innerhalb der Gesamtmatrix an.Sofern die Teilchenoberfläche nicht ideal glatt ist, kann die tatsächliche Oberfläche berücksichtigt werden, wenn ein ent sprechender Vergrößerungsfaktor bekannt ist
Für Agglomerate aus Teilchen mit beliebiger Korngrößenverteilung n(x) mit x = dP gibt Rumpf eine erweiterte Form der Zugfestigkeitsgleichung an [126].
In diesem Fall sind die vereinfachten Überlegungen der gleich verteilten Werte der Haft-kraft pro Partikelkontakt und eines mittleren Erwartungswertes der Koordinationszahl, die Formel 2zugrunde liegen, nicht mehr gültig.
Bei Partikeln mit unterschiedlicher Größe hängt die Haftkraft von der Teilchengröße und der Größe der jeweiligen Haftpartner ab, also von x und von n(x).
Danach ist die ideale, einachsige Zugfestigkeit, die als Zerreißfestigkeit definiert ist gleich

Die Anwendung und Integration der Formel 34ist nur möglich, wenn die Abhängigkeit der Koordinationszahl und der Haftkraft von der Teilchengröße und verteilung bekannt sind.
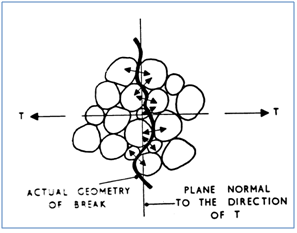
Ein weiterer Ansatz zur Ermittlung der Zugfestigkeit wird von Cheng [128] beschrieben.Bei diesem Ansatz werden die Packungsdichte und die Partikelverteilung berücksichtigt. Die interpartikulären Kräfte werden dadurch berücksichtigt, dass alle möglichen kraft auslösenden Mechanismen wie Van der Waals, Flüssigkeitsbrücken und elektrostatische Kräfte in Abhängigkeit der Oberflächenentfernung t in der Funktion h(t) enthalten ange nommen werden.Unter dem Einfluss einer einachsigen Zugspannung verläuft die Versa-gensebene unregelmäßig entlang der getrennten Partikelpaare, wodurch ein Bereich eines Versagensvolumens entlang der unregelmäßigen Bruchlinie geformt wird, siehe Abbildung 81.
Abbildung 81: Versagensebene und Partikelhaftkräfte eines Agglomerates unter
zentrischerZugbelastung [128].
Innerhalb des Versagensvolumens befindet sich unter Annahme einer zufälligen Verteilung der Partikel die gleiche Funktion der Partikelverteilungsdichte wie in der gesamten Agglomeratmatrix. Unter Berücksichtigung der vorhandenen Oberflächenimperfektionen der Partikel werden Annahmen zur Geometrie der Mikrokontakte zwischen den Partikeln bezüglich der Gesamtkontaktfläche und der Oberflächenentfernung getroffen.
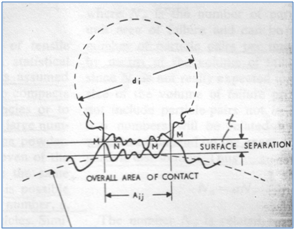
Abbildung 82: Kontakt zweier Partikel unter Berücksichtigung von Oberflächen
imperfektionen; Pkte. M: Kontaktpunkte Pkt. N: Kontaktpunkt bei weiterer Annäherung derOberflächen durch Deformation [128]
Bei diesem Ansatz wird die Zugkraft T aus der Summe aller Einzelkontaktflächen Aij(Abbildung 82) in Abhängigkeit von der Zugspannung h(t) und der Oberflächendistanz t der Partikelpaare berechnet. Da sowohl Aij als auch die Oberflächendistanz t durch Rechenansätze oder materialspezifische Gesichtspunkte kaum beschrieben werden können, wurden für diese Größen stark vereinfachte Abschätzungsgleichungen aufgestellt, die wiederum mit empirischen Proportionalitätskonstanten versehen sind.
Die Partikelpaare in der Bruchlinie werden hier über einen Ansatz aus der Wahrscheinlichkeitsrechnung abgeschätzt.
Mit

wird der Anteil der Partikelpaare bestehend aus den Partikeln i und j aus deren Fraktionsanteilen ni, nj an der Gesamtpartikelzahl ermittelt.Als Ergebnis seiner Arbeiten machte Cheng zwei wesentliche Faktoren als Einflussgrößen auf die Zugfestigkeit von Agglomeraten aus: die Partikelgrößenverteilung und die Abhängigkeit der Interpartikulären Kräfte vom Abstand der Partikeloberflächen, hervorgerufen durch Oberflächenrauhigkeiten. Dieser Faktor ist maßgeblich dafür verantwortlich, dass Zugfestigkeiten zum Teil erheblich variieren, obwohl nur geringe Dichteunterschiede im Agglomerat festgestellt wurden.
Es existieren noch viele weitere Modelle über die Ermittlung der Spannungen in Haufwerken und Packungen aus feuchten Partikeln [129], [130] die für Fälle von Partikelverteilungen mit unterschiedlichen wirkenden Kräften je Kontaktfall sehr aufwändig werden und dennoch nur Näherungslösungen liefern. Diese versuchen alle, durch zunehmende Komplexität der Annahmen eine scharfe und realistische Darstellung der Zugfestigkeit zu ermöglichen, jedoch laufen die Gegenüberstellungen mit Versuchsergebnissen immer darauf hinaus, dass Korrektur und Anpassungsfaktoren erforderlich sind, um die theoretischen Berechnungen mit den praktischen Resultaten in annähernde Übereinstimmung zu bringen. Allen Ansätzen gemeinsam ist, dass sie bisher nicht vermocht haben, einen theoretischen Zusammenhang des Zug Dehnungsverhaltens mit bekannten Eingangsgrößen der Partikelverteilung, anzahl und oberflächengestalt zu schaffen.Daher greifen auch neuere Arbeiten [131] wiederholt auf die einfache Formel von Rumpf zurück (Formel 33) und wählen mittlere Durchmesser und angenäherte Koordinationszahlen aus, um Abschätzungen der zu erwartenden Zugfestigkeit vorzunehmen.