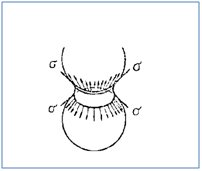
Entgegen der dargestellten Unterscheidung in drei Mechanismen (echte Kohäsion, Kapillarkohäsion, Strukturwiderstand), beschränkte sich Wierig [20] in den theoretischen Untersuchungen darauf, die kapillare Kohäsion für das Entstehen der Gründruckfestigkeit anzusetzen sowie den Reibungswinkel als Einflussfaktor für den Strukturwiderstand. Die kapillare Kohäsion entsteht durch das Zwickelwasser an der Berührungsstelle zweier benetzter Körper (siehe Abbildung 32).
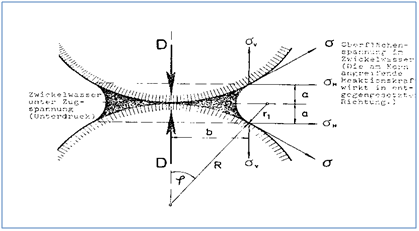
Abbildung 32: Spannungen in der Oberfläche des Zwickelwassers [20]
Voraussetzung für das Wirken der Oberflächenspannung ist das Vorhandensein von Luft an den Grenzflächen der Flüssigkeitsbrücke, d.h. ein Dreiphasensystem. Ein gesättigtes Zement Wasser Gemisch ist lediglich ein Zweiphasensystem, es bestehen darin keine isolierten Flüssigkeitsbrücken und es fehlen die für das Wirken der Oberflächenspannung notwendigen Grenzflächen WasserLuft. Die im Zwickelwasser vorhandene Zugspannung überträgt sich auf die benachbarten Flächen und drückt sie, wie in Abbildung 33 dargestellt, gegeneinander.
Abbildung 33: Druckkräfte zwischen zwei benetzten Kugeln [122]
Dabei reduziert sich die Höhe der Zugspannung mit zunehmender Größe des Zwickels, z.B. durch Hinzufügen von Wasser. Über eine Erweiterung der Modellvorstellung für beliebig gekrümmte Flächen, wie sie an Gesteinskörnern vorliegen, wird die Zugfestigkeit eines Dreiphasensystems theoretisch abgeschätzt.Aus dieser Modellvorstellung ergibt sich, dass die Haftung zwischen zwei Zementkörnern kleiner ist als die zwischen einem Zement und einem Gesteinskorn. Dem Zementleim fällt dadurch der Charakter des schwächsten Gliedes zu. Daher erfolgte der rechnerische Nachweis der Zugfestigkeit bei Wierig [20] für den Zementleim (siehe Kap. 2.4.3), ebenso wie die Herleitung der theoretischen Druckfestigkeit aus der errechneten Zugfestigkeit des Zementleimes mit Hilfe des Mohr´schen Spannungskreises.
Die Berechnung der Zugfestigkeit erfolgte unter den Annahmen, dass Zementkörner als Kugeln mit einem mittleren Durchmesser betrachtet werden, die in der lockersten Lagerung gepackt sind.
Für kleine Benetzungswinkel Φ wird der Verlauf des Meniskus in der Schnittebene als Kreisbogen angenommen. Die Druckkraft zwischen zwei Partikeln ist dann
D = 2*π*σ*R Formel 1
Die mittlere Oberflächenspannung σdes Wassers bei 20 °C liegt bei 72,75*10-3N/m.
Für die theoretische Grünzugfestigkeit bei lockerster Lagerung bestimmt Wierig
ßZ= (π*σ)/d Formel 2
d = mittlere Korndurchmesser des Zementes
Bei einem mittleren Partikeldurchmesser von 22µm liegt die Zugfestigkeit bei 1,04 N/cm2. In den wenigen durchgeführten Zugversuchen wurden ca. 0,5 N/cm2 erreicht, was als befriedigende Übereinstimmung interpretiert wurde.
Anhand der rechnerischen Grünzugfestigkeit wurde die Gründruckfestigkeit mit Hilfe des Mohrschen Spannungskreises berechnet.Der für die Druckfestigkeit erforderliche Reibungswinkel ρ wurde berechnet aus demGleitwinkel ∝, unter dem die Probekörper im Druckversuch abscherten zu
ρ = (90°-2*∝) Formel 3
Dabei lagen die Gleitwinkel der Probekörper im Mittel bei∝ = 27°. Die ermittelten Gleitwinkel streuten sehr stark und erwiesen sich ebenfalls als abhängig von der Verdichtung und dem Wassergehalt.
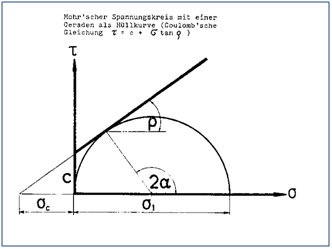
Abbildung 34: vereinfachte Darstellung des Spannungskreises nach Mohr [20](σ1=βDr=Druckspannung, σC =βZ= Zugspannung)
Die Gründruckfestigkeit βDr wurde unter der Annahme der Darstellung in Abbildung 34 wie folgt berechnet:
ß= (2*ßZ*sin“ ρ“ )/(1-sin“ ρ“ ) Formel 4
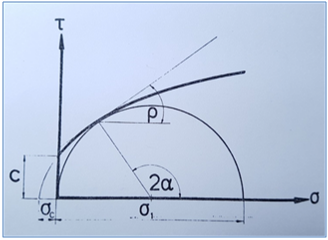
Dabei errechnete Wierig eine Gründruckfestigkeit von 4 N/cm2. Die gemessenen Gründruckfestigkeiten lagen bei etwa 11 N/cm2.Wierig schlägt daher vor, sich am Mohrschen Spannungskreis mit gekrümmten Hüllkuren zu orientieren, da aus der Bodenmechanik bekannt ist, dass für feuchte Böden die Einhüllenden keine Geraden, sondern zur x Achse konkav gekrümmte Kurven sind, siehe Abbildung 35.
Abbildung 35: Mohrscher Spannungskreis mit Parabel als gekrümmter Hüllkurve [20] für feuchte Böden
Dies führt zu einem größeren Verhältnis von Druck–zu Zugfestigkeit von ca. 11, so dass er eine genaue Übereinstimmung feststellt.
Der Einfluss der Verdichtung auf die Gründruckfestigkeit wird erklärt, indem auf eine Zunahme der Berührungsstellen der Feststoffe und damit auch eine Erhöhung der Zahl der Menisken mit dichter werdender Lagerung verwiesen wird.
Bei dem mittleren Durchmesser der Zementpartikel und der daraus resultierenden Anzahl pro Flächeneinheit wurde der Wasserfilm um die Zementpartikel nicht mit berücksichtigt. Jedoch führen die Wasserfilme dazu, dass sich der anzusetzende Durchmesser je Partikel vergrößert und sich die Packungsdichte, d.h. die Nähe der einzelnen Körner zueinander verringert.
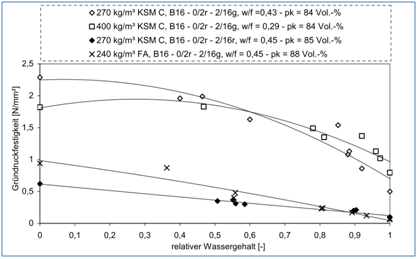
Bornemann [22] kommt zu einer von Wierig [20] komplett gegenteiligen Schlussfolgerung. Danach geht von der Kapillarität gar kein Einfluss bzw. lediglich ein ganz geringer Einfluss aus. Dies begründet er mit dem Ergebnis von Rücktrocknungsversuchen, die an Kalksteinmehl vorgenommen wurden, siehe Abbildung 36. Bei vollständiger Rücktrocknung war die Gründruckfestigkeit bei allen vier überprüften Zusammensetzungen am höchsten. Daher schließt er die Haftkräfte bedingt durch Kapillarität als Einfluss aus, weil sowohl im trockenen wie auch im gesättigten Zustand keine Kapillarkräfte wirken können. Der Reibungswinkel und die innere Verzahnung spielen nach seiner Einschätzung die wesentliche Rolle bei der Gründruckfestigkeit.
Abbildung 36: Rücktrocknungskurven von Mischungen ohne Zement mit unterschiedlichen
Gehalten an Kalksteinmehl und einer Mischung mit Flugasche als Vergleich [22]
Die Berechnung der Gründruckfestigkeit erfolgte bei Bornemann nicht über eine theoretische Herleitung der Zugfestigkeit wie bei Wierig.Die Ermittlung der Kohäsion und des Reibungswinkels erfolgte anhand von Rahmenscherversuchen. Dabei wurden keine erdfeuchten Betone untersucht, sondern lediglich Gemische aus Feinquarz, Sand und Kies bis 8 mm um die Bildung von Hydratationsprodukten während des relativ aufwändigen Rahmenscherversuches zu vemeiden.
Die Tragfähigkeitsberechnung erfolgte als freistehender Bodenkörper ohne seitliche Abstützung nach Rankine, wobei die horizontale Spannung durch die Kohäsionsspannung ersetzt wurde. Dabei ergab sich die Gründruckfestigkeit zu
σ1= 2c/tan(45-φ/2) Formel 5
mit c = Kohäsion und Φ = Reibungswinkel [°], beides aus Rahmenscherversuchen.
Jedoch lagen die errechneten Gründruckfestigkeiten erheblich unter den gemessenen, was dadurch erklärt wurde, dass die o.a. Formel nur für sehr schlanke Probekörper gelte.
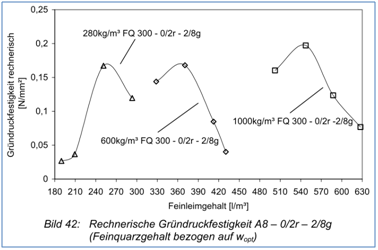
Abbildung 37: von Bornemann ermittelte, rechnerische Gründruckfestigkeit einer Rezeptur ohne Zement mit unterschiedlichen Gehalten an Quarzmehl und Wasser –ausgedrückt über den Leimgehalt [22]
Die Werte in Abbildung 37 sind zu vergleichen mit den in Abbildung 26 enthaltenen Versuchsergebnissen, die an erdfeuchten Betonen mit Zement ermittelt wurden.
Bei Analyse der Rahmenbedingungen, mit denen die rechnerischen Ausgangsgrößen Kohäsion und Reibungswinkel ermittelt wurden, insbesondere ohne Einsatz von Zement, fällt auf, dass die Gründruckfestigkeiten in Abbildung 26 deutlich größer sind. Eine mögliche Erklärung liegt darin, dass die Haftkräfte zwischen den Zementpartikeln deutlich größer sein können als zwischen Quarzpartikeln, mit denen die Kohäsion und der Reibungswinkel im Rahmenscherversuch ermittelt wurde.
Dadurch ist die Kohäsion höher und auch der Reibungswinkel, so dass höhere gemessene Festigkeiten als die errechneten die Folge sind.
Insgesamt steht bei Bornemann der Reibungswinkel, der die Verzahnung der Partikel untereinander ausdrückt, an erster Stelle als Erklärung für die Gründruckfestigkeit. Bereits geringe Schwankungen des Reibungswinkels durch z.B. Zugabe runder Partikel oder höheren Leimgehalten führen zu großen Unterschieden bei der Gründruckfestigkeit. Die Kapillarkohäsion ist aus seiner Sicht vernachlässigbar, die Auswirkungen echter Kohäsion hält er für möglich, jedoch findet sie in seinen Berechnungen keinen Eingang. Er weist darauf hin, dass erdfeuchte Betone im Allgemeinen einen hohen inneren Reibungswinkel und hohe Kohäsionskräfte aufweisen. Bei nur geringen Veränderungen sinkt die Tragfähigkeit stark ab. Für solche Systeme seien Rahmenscherversuche zu ungenau, um diese geringen Abweichungen messtechnisch erfassen zu können [22].