Wie in Kap.2.4.2 beschrieben wird, gehen von den Oberflächenbeschaffenheiten der Partikel Einflüsse auf die Ausbildung und Übertragung der interpartikulären Kräfte aus.
Die meisten bestehenden Modellvorstellungen, die überwiegend aus den Jahren 1950 1970 stammen, gehen aus Gründen der Vereinfachung überwiegend von ideal glatten Oberflächen und kugeligen Formen aus. Von einer Kugelform sind reale Zementpartikel sehr stark abweichend, wie Abbildung 54 exemplarisch darstellt. Bedingt durch den Mahlvorgang des Klinkers und evtl. zugegebener weiterer Stoffe weisen die Partikel eine unregelmäßige, kantige Form auf, die aus dem Zerkleinern von größeren Stücken in kleinere folgt.
Abbildung 54: Partikelformen von trockenem Portlandzement, aus van Breughel [74]
Je nachdem ob die Zerkleinerung überwiegend schlagend erfolgt, was bei Korngrößen über 30 µm vermutet wird oder eher reibend bei den darunterliegenden Korngrößen, können die Partikelformen in Abhängigkeit der Korngröße Unterschiede aufweisen. Hierzu liegen jedoch keine gesicherten Erkenntnisse vor, so dass van Breughel [74] davon ausgeht, dass die Partikelform als von der Partikelgröße unabhängig angesehen werden kann. Während Zertrümmerungsbrüche, die durch sehr hohe Beanspruchungsintensitäten hervorgerufen werden, meist kantige Partikel produzieren, führen Abrasivbrüche zu abgerundeten Partikeln [75]. Daher haben die Mahlsysteme für Zemente, Gutbett Walzenmühle, VertikalWälzmühle und Kugelmühle, einen Einfluss auf die Kormform des jeweiligen Zementes.Zement besteht aus kantigen Partikeln mit nicht exakt definierter Geometrie. Die tatsächliche Oberfläche einzelner Zementpartikel ist aufgrund der Mahlprozesse zerklüftet und mit Tal und Sattelpunkten versehen, die in der Regel scharfkantig geformt sind.
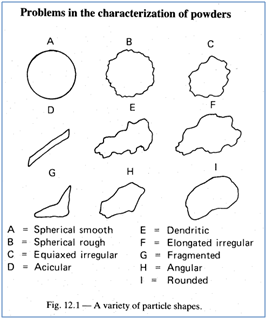
Abbildung 55: Unterschiedliche Partikelformen nach Igwe [76]
Auch eine Beschreibung der Partikelformen gemäß Abbildung 55 [76] ist lediglich eine Annäherung, anhand derer Zement z.B. eher in die Katekorie H „Angular“ eingeordnet werden kann und Flugasche in B „Spheric rough“. Die eigentliche Partikelform beeinflusst das Verhalten bei Verdichtung, die mögliche Packungsdichte sowie den Abstand der Partikeloberflächen und die Gesamtkontaktfläche, die möglich ist.
Eine wesentliche Größe bei der Berechnung von Spannungen in Agglomeraten ist die Zahl der benachbarten, sich berührenden Partikel, genannt Koordinationszahl. Die Koordinationszahl k gibt die Zahl der Berührungspunkte eines Teilchens mit Nachbarteilchen und damit die Zahl der Kraftübertragungspunkte an. Sie ist abhängig von der Raumausfüllung Φ, auch bezeichnet als Packungsdichte, die bei trockenen Partikelsystemen errechnet wird aus dem Anteil des Volumens aller Partikel am Gesamtvolumen, das die Packung beansprucht.Der Hohlraumanteil am Gesamtvolumen des Stoffsystems wird als Porosität ε bezeichnet (ε = 1-Φ).
Sämtliche Faktoren, die einen Einfluss auf die Porosität haben, wie z.B. Partikelgröße und verteilung, beeinflussen auch die Koordinationszahl.Im Falle der Kanonenkugeln der Abbildung 41 beträgt die Koordinationszahl für monodisperse Kugelnin sog. Hexagonal dichtester Packung raumzentriert k = 12. Die empirische Bestimmung der Koordinationszahl einer Partikelschüttung bzw. eines Agglomerates bestehend aus Kugeln verschiedener Größe oder gar beliebig geformten Teilchen ist bislang nicht eindeutig reproduzierbar erfolgt.
In solchen Packungen bestehen außerdem nicht nur Berührungspunkte, sondern auch Nahpunkte. Nahpunkte bestehen dann, wenn die Nachbarteilchen bei Betrachtung eines bestimmten physikalischen Mechanismus gerade noch miteinander in Wechselwirkung treten, ohne dass ein Massenkontakt stattfindet.
Aufgrund der unterschiedlichen Reichweite der in Kap.2.4.2 beschriebenen Kraftmechanismen existieren also in Abhängigkeit der Haftursache unterschiedlich viele physikalische Nachbarn.In mehreren Arbeiten werden Annahmen bezüglich der Koordinationszahlen zugrundegelegt.Ein Überblick über Koordinationszahlen in Abhängigkeit des räumlichen Verteilungsmodells in einer Matrix ist in [77] enthalten, sie liegenbei gleich großenKugeln zwischen 6 (loose Packung) und 12 (dichteste Packung). Neben der Frage, ob alle Partikel gleich groß sind oder Partikel in verschiedenen Größen vorhanden sind, geht auch ein Einfluss von einer umgebenden Behälterwand aus, der von dem Verhältnis der Behältergröße zur Partikelgröße abhängt.

Iwadate [78] wählt für seine Anwendung der Zugfestigkeitsgleichung von Rumpf auf die Fluidisierbarkeit von Pulvern die Koordinationszahl
k = 1,61ε-1,48 (ε ≤ 0,82)für Agglomerat-zu-Agglomerat-Kontakte.Auf Suzuki [79] geht ein Modell zur Bestimmung der Koordinationszahl einer Mehrkomponen¬ten Kugelschüttung mit polydispersen Partikeln zurück. Dabei wird mit dem Anteil der rechnerischen Partikelanzahl je Fraktion an der Gesamtpartikelanzahl der Oberflächen anteil jeder Partikelfraktion ermittelt. Es zeigte sich, dass bei drei verscheidenen Ansät zen der Partikelverteilung (Log-uniform, Rosin-Rammler, Andreasen (Gaudin-Schumann)) die Koordinationszahlen immer in der Nähe von 6 lagen.
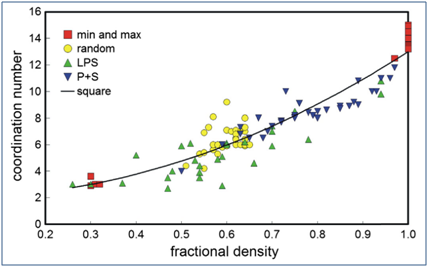
Insgesamt wurde sich bisher in zahlreichen Arbeiten damit beschäftigt, eine Vorhersage zu entwickeln. German [80] hat über 113 Arbeiten ausgewertet und kommt zu einem sehr über sichtlichen Abschluss. Nach Abbildung 56 stellt sich unter Berücksichtigung aller von German ausgewerteten Ergebnisse ein annähernd linearer Zusammenhang zwischen Packungsdichte und Koordinationszahl ein, obwohl verschiedenste Zustände zusammen aufgeführt wurden: Zufallspackung (random), verdichtet gesintert (P+S), gesintert mit Flüssigphase (LPS).
Abbildung 56: Zusammenhang zwischen Packungsdichte und Koordinationszahl nach einer
umfassenden Literaturauswertung und Modellierung nach German [80]
Jedoch führen stark haftende Partikel sowie Partikel mit hoher Reibung durch Rauhigkeiten oder Kornform zu geringeren Dichten und damit auch zu geringerenKoordinationszahlen als nach Abbildung 56.
Bei den theoretischen Betrachtungen zur Optimierung von Packungsdichten, wie sie z.B. Teichmann [81] bei fließfähigen Suspensionen durchführte, wird vorausgesetzt, dass sämtliche Partikel trocken sind und keine Flüssigkeit vorhanden ist oder dass es sich um eine Suspension handelt, bei der die Flüssigkeit zusammen mit feinen Partikeln die Rolle des Abstandshalters zwischen den einzelnen gröberen Partikeln übernimmt. Ebenso werden ideal runde Partikel vorausgesetzt. Im EF Bereich, in dem alle Partikeloberflächen mit Wasser benetzt sind, vergrößern sich zum Einen die Partikeldurchmesser um den unbeweglichen Anteil sterischen Wassers, von dem sie umgeben werden. Zum Anderen werden durch die Haftkräfte durch Flüssigkeitsbrücken und durch evtl. elektrische Aufladungen während des Mischprozesses sowie durch Van der Waal Kräfte die Partikel nicht die ideal theoretisch dichteste Lagerung zueinander einnehmen können. Sie beginnen vorher aufgrund der Haftkräfte zu agglomerieren, d.h. sich zu punktuellen Partikelhaufwerken zusammen zu heften.
Auch in trockenen Partikelhaufwerken wird die theoretisch dichteste Packung, die durch viele Optimierungsansätze versucht wurde, zu erreichen, nicht erzielt, weil die Haftkräfte der feinen Partikel < 1 mm größer sind als deren Gewichtskraft und daher ein Hineingleiten in noch unbesetzte, leere Matrixräume nicht gelingt, weil sie vorher an Haftpartnern agglomerieren
Die hier dargestellten Zusammenhänge verdeutlichen, dass die Partikel von Zement weder ideal glatte Oberflächen noch runde Partikelformen aufweisen. Dadurch wird die theoretische Abschätzung der Koordinationszahl erschwert, was bereit durch das polydisperse Auftreten (Körner unterschiedlicher Größe) der Fall ist. Somit ist eine Berechnung einer Koordinationszahl unter den realen Bedingungen wie sie bei Zementen vorliegen, bislang nicht möglich.